On the Complexity of a Legitimate Social Choice
In the last chapter of Social Choice and Individual Values (or the penultimate chapter of the 1963 edition), Kenneth Arrow considers the problem of agreeing over a social welfare function (SWF), or more generally a decision rule, for collective choice. Arrow’s idea (which will be later developed further by Amartya Sen) is that the decision rule may itself be an object of the preferences of individuals, especially if these preferences are analyzed as values. Obviously, the choice of a SWF is itself a collective choice. Is it possible to embed in the social choice framework the (collective) choice of a SWF without being trapped in some sort of infinite regress?
Arrow proposes to characterize social states (the ultimate objects of the collective choice) as vectors of characteristics. So social state x can be described as a vector (x1, x2) with x1 itself a vector that describes all the relevant characteristics except for the way they have been collectively chosen and x2 is the specific decision rule from which x has been collectively chosen. Usually, individual preferences in a social choice framework are only defined for x1, but there is no formal difficulty in extending their domain of definition. An obvious worry here however is that the collective choice of a social state x depends on the decision rule that is used, and which decision rule is used depends on a collective choice. Arrow argues however that there is no risk of circularity here. Still, a potentially infinite regress is lurking: we may imagine that individuals also have preferences over decision rules to choose decision rules, decision rules to choose decision rules to choose decision rules, and so on. Arrow’s solution consists in assuming that, at the bottom, there must be a unanimous agreement over some n-level decision rule. He adds that such agreement “seems to be implicit in every stable political structure”.
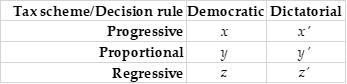
More than stability, I think that Arrow’s point is about legitimacy. A social choice can only be considered legitimate if it is made based on a SWF that everyone accepts. Obviously, this is especially true for those persons who would have preferred a different social choice. Now, intuition suggests that the requirement of legitimacy makes social choices even more complicated to make, on top of the formal impossibilities that Arrow and others have discovered. Let’s consider a simple example to understand the difficulties. Suppose a 5-individual society that has to settle on a tax scheme. Three tax schemes are put on the agenda: a progressive scheme, a proportional scheme, and a regressive scheme. Suppose moreover that the collective choice can be made along with two different decision rules: a democratic rule and a dictatorial rule. On the former, the scheme is chosen based on a Condorcet procedure. On the latter, one of the five individuals is randomly picked, and this individual’s preferred scheme is chosen. We thus have a state space W of 6 social states from which to choose:
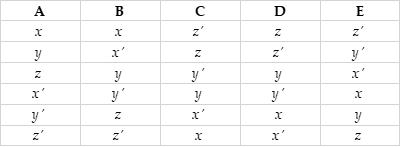
The individuals’ preferences over W are assumed to be reflexive, complete, asymmetric, and transitive, and as follows
The Condorcet procedure generates the following social preference ordering (only keeping the social states that can be chosen with a democratic rule):[1]
Depending on whose individual is picked, the dictatorial rule will lead to the choice of x’ (with probability 2/5) or z’ (with probability 3/5).
By definition, the two SWF will not lead to the same social choice (as each decision rule eliminates one-half of the social states). More importantly, which SWF is used also makes a difference about which scheme will be chosen, as the democratic rule selects the progressive scheme, while the dictatorial rule is more likely to choose the regressive scheme. The point is that in this example, there is no Arrowian agreement on a decision rule. This is true whatever the way we may understand the concept of “preferring a decision rule”:
On this definition, individual A strongly prefers the democratic rule to the dictatorial rule, while E has a contrary preference. But neither B, C, nor D have any preference in this sense. In the same way, A, B, and D have a weak preference for the democratic rule, while C and E have a weak preference for the dictatorial rule. So there is no agreement over a SWF independently of the definition we use.
Arrow’s suggestion in this situation is to go one level up and to look for individuals’ preferences over decision rules for decision rules. But is there any real reason to suspect that agreement will be found at a higher level? The answer may depend on the specific social choice problem under consideration but at least in some cases, it must be negative. Instead of giving up, we may look for a more fundamental agreement. For instance, it is not obvious how an individual’s preference for a SWF is related to her preference for a tax scheme. As an illustration, individuals A and B, given what they know or believe about others’ preferences, may expect that the democratic rule is more likely to deliver their preferred progressive scheme. In other words, the “revealed” preferences over SWF may be the result of some sort of strategic manipulation. So, let’s try to neutralize this possibility. A possible approach is the following. A social state x may be redescribed as follows:
This idea is that, from individual i’s perspective, a social state consists of three (sets of) components: her personal situation, the personal situation of every other person, and a decision rule through which the state has been chosen. One way to neutralize the effect of individuals’ preferences over tax schemes on their preferences over SWF is to require that the appropriate informational basis is constituted by the individuals’ extended preferences over tax schemes. If N is the of individuals, then extended preferences are defined over the Cartesian product W x N. They are of the form,
meaning that individual k prefers to be individual i in social state x than individual j in social situation y. Arrow himself, as well as John Harsanyi through a different approach, have argued that extended preferences must be identical in a population. In other words, all individuals would rank the personal situations in the same way. In this case, that would seem to indicate that differences regarding the preferences over SWF would not be due to extended preferences over tax schemes. Presumably, that would increase the probability that individuals agree on the decision rule to be used.
This approach hardly provides a solution, however. First, the claim that extended preferences must be identical is doubtful, for reasons that would be too long to develop here. Second, even if we grant this claim, it doesn’t follow those individuals will agree on the ranking of the vectors of personal situations. It is easy to see why. In the social choice framework, the ordering of social states depends on two components: an informational basis and an aggregation rule. Assuming that extended preferences are identical in the population means that everyone agrees on the informational basis. But this doesn’t settle which aggregation rule should be used. This, of course, depends on the decision rule, i.e., the very point on which we are desperately searching for an agreement! Of course, we may want to assume that individuals’ extended preferences also cover the second component of the vectors x and that they are identical. But not only it is highly unlikely to discover formal proof for this. This suggestion leads us on the verge of self-contradiction, for assuming that at the bottom there must be a fundamental agreement on everything defeats the very purpose of making social choices – and of doing social choice theory!
In the end, we may just stipulate as Arrows seems to suggest that we are living in politically stable societies, a postulate that is every day harder to endorse. Another approach, more promising, is to consider that the analysis of the normative basis of SWF must be made outside social choice theory, or more exactly by appealing to conceptual and theoretical resources adding a normative content to this theory. The reader – if there is still one at the end of this long essay – may then be interested in my book project that is slowly progressing, and which precisely pursues this route.
[1] The complete ordering is
We should not worry about the (apparent) contradiction that a dictatorial choice may be democratically preferred.